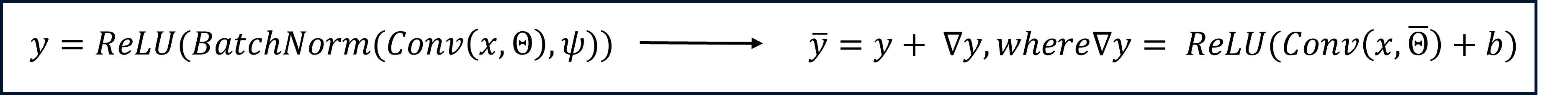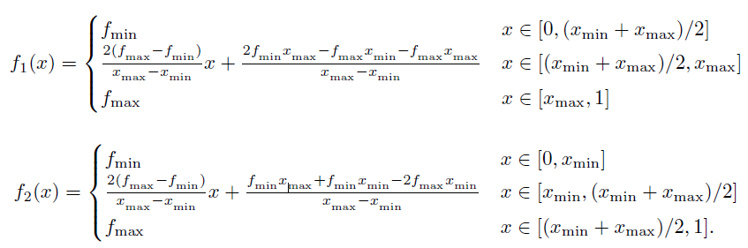Don't trust your eyes: on the (un)reliability of feature visualizations

Don't trust your eyes 논문 리뷰

Posted Apr 30, 2025

views 15 min read

Don’t trust your eyes: on the (un)reliability of feature visualizations (arXiv)
Year : 2023
Authors : Robert Geirhos et al.
Conference : ICML

Introduction

Hegenlian dialectic.

“Interpretability”, “Reliability”

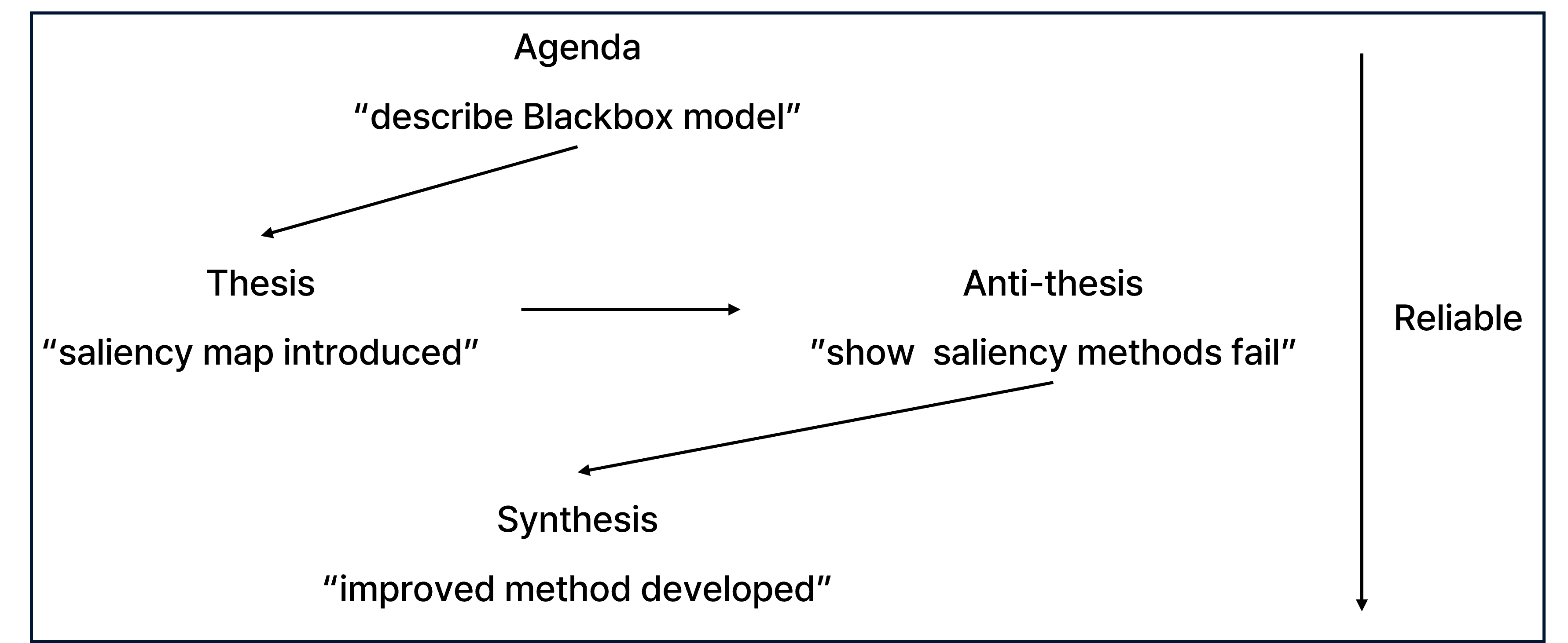
Hegelian dialectic

딥러닝 해석가능성 해법들은 헤겔의 변증법(Hegelian Dialectic)처럼 발전해 왔다. 어떤 방법이 등장(thesis)하고, 그 한계가 지적되며(antithesis), 새로운 개선된 방법(synthesis)으로 이어지는 순환을 보인다. 본 논문은 그 중에서도 Activation Maximization 기반 Feature Visualization이 정말 신뢰할 수 있는지에 대한 의문을 던진다.

Feature Visualization

출처 : https://distill.pub/2017/feature-visualization/, https://distill.pub/2018/building-blocks/.

Feature Visualization은 뉴런 또는 채널을 극대화하는 이미지를 생성하여 신경망이 무엇을 “보고” 있는지를 직관적으로 보여주는 방법이다.

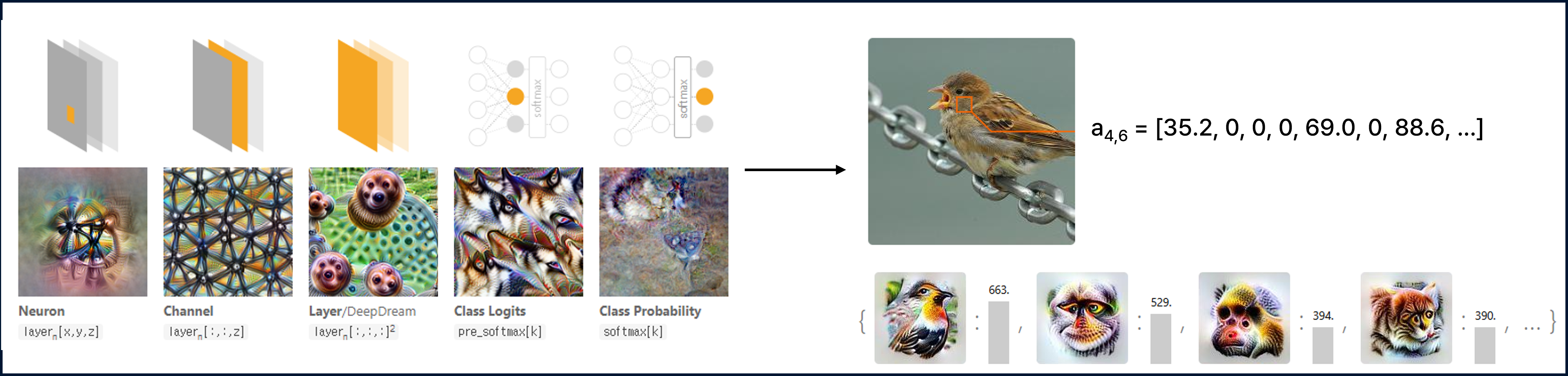
Activation Maximization Overview.

Activation Maximization은 신경망 내부의 특정 뉴런(혹은 채널, 레이어 출력 등)을 가장 크게 활성화시키는 입력 이미지를 찾는 최적화 기반의 해석 방법이다다.
이 과정을 통해 해당 뉴런이 어떤 입력에 반응하는지를 시각적으로 이해할 수 있다.

\[x^* = \arg\max_x f(x)\]

주요 아이디어로는 모델에 존재하는 어떤 뉴런이 가장 반응하는 입력을 역으로 생성하는 방식이다.

$f(x)$: 특정 뉴런이나 채널의 출력 (activation)
$x^*$: 해당 뉴런을 가장 크게 활성화시키는 입력 이미지

전체 과정을 보면, 무작위 노이즈 이미지를 초기 입력 $x_0$로 설정하여 초기화를 진행하고 그 다음 해당 뉴런의 출력값 $f(x)$를 최대화하도록 Forward Process를 진행한다. 그 후 입력 이미지 $x$에 대해 gradient ascent를 수행하여 Backward Process를 진행한다. 마지막으로 현실적인 이미지 형태를 유지하기 위해 regularization을 추가한다.

\[\hat{x} = \arg\max_x \left( f(x) - \lambda \cdot R(x) \right)\]

$R(x)$: 이미지에 대한 규제 항 (e.g. smoothness, 자연스러움)
$\lambda$: 규제 강도

최종 결과는 직관적으로 결과 이미지 $\hat{x}$는 모델이 해당 뉴런이 어떤 특징을 보고 있는지를 시각적으로 보여준다.

예: 특정 채널이 곱슬머리, 푸들, 강아지 눈을 감지한다면, $\hat{x}$는 그러한 패턴을 담게 된다.

Motivation

How reliable are feature visualizations?

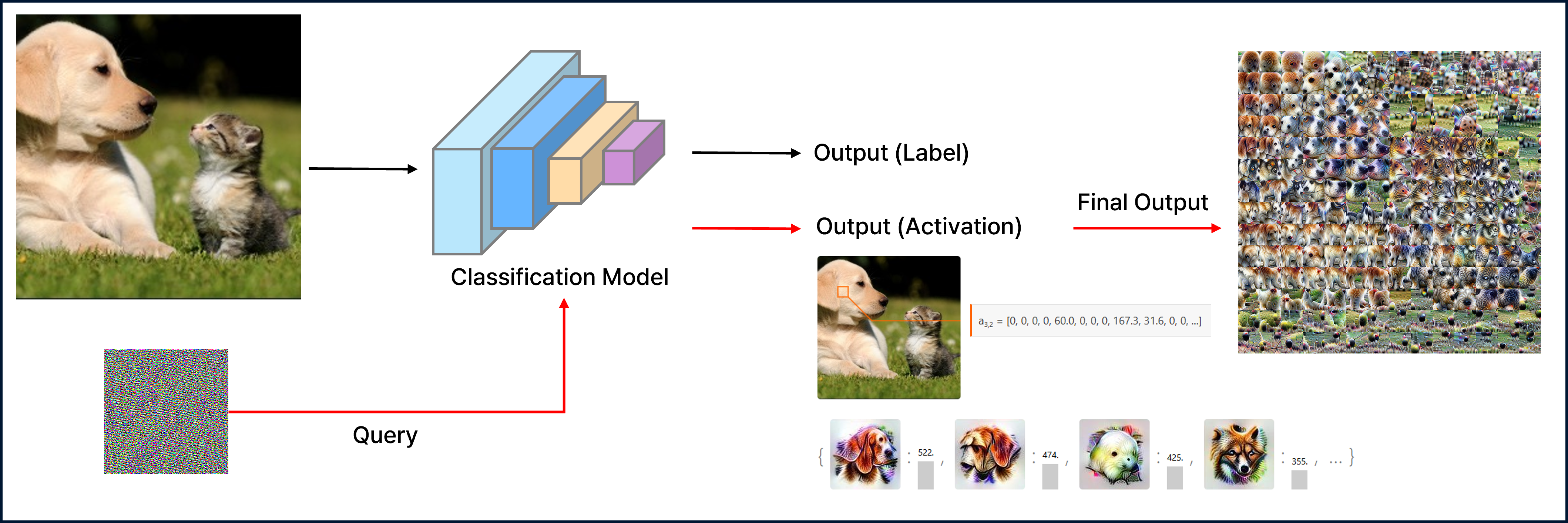
Feature visualization은 일반적으로 무작위 노이즈 이미지를 시작점으로 하여, 특정 뉴런 A가 가장 강하게 활성화되도록 입력 이미지를 반복적으로 최적화하는 방식으로 이루어진다. 본 논문에서는 이러한 시각화 기법이 얼마나 쉽게 조작될 수 있는지를 보여주며, feature visualization 자체의 신뢰성에 대해 경각심을 불러일으킨다. 논문에서는 네트워크 구조를 조작함으로써 시각화 결과를 속이는 것이 가능하다는 것을 증명하고, 이를 통해 feature visualization을 대상으로 한 최초의 interpretability circumvention attack을 제안한다. 이 공격 시나리오는 모델 백도어 삽입, 가중치 조작, 학습 데이터 중독 등 일반적인 머신러닝 공격과 유사한 맥락에서 설명될 수 있다.

Proposed Method

Manipulating feature visualization through a fooling circuit

Figure 1: 서브 네트워크 삽입 결과.

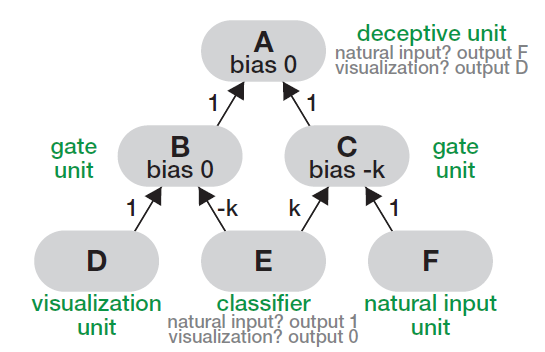
본 논문에서는 시각화의 신뢰성에 대한 경각심을 불러일으키기 위해 서브 네트워크를 삽입하여 Natural input에 대해서는 원래대로 동작하며 Feature visualization에서는 다른 반응을 하게 만드는 구조인 fooling circuit을 제안한다.
Figure 1은 서브 네트워크인 fooling circuit을 추가했을 때 feature visualization을 통해 생성되는 이미지를 완전히 조작할 수 있음을 보여준다.
실제로, 특정 뉴런이 ‘모나리자’나 ‘강아지’와 같은 전혀 무관한 패턴을 출력하도록 설계할 수 있으며, 이는 원래 모델의 성능(예: ImageNet top-1 정확도)에는 거의 영향을 주지 않는다.

Figure 3: fooling circuit.

fooling circuit의 구조
- A : 속이려는 대상 (feature visualization 대상)
- F : natural input에 대해 A가 따라야할 원래 동작
- E : input이 natura인지 visualization 대상인지 구별하는 분류기
- D : visualization 대상에 대해 A가 따라야 할 속임 동작
- B,C : ReLU 기반 경로 선택 동작

\[\text{natural input} \Rightarrow A = F, \quad \text{visualization input} \Rightarrow A = D\]

fooling circuit의의 동작
1. natural
  - E에 의해 natural 이다 라고 판단
  - B 활성화
  - C 차단
  - A는 F 처럼 동작
2. visualization
  - E에 의해 visualization 이다 라고 판단
  - C 활성화
  - B 차단
  - A는 D처럼 동작

이처럼 fooling circuit은 단일 분류기를 통해 입력 분포를 구분하고, 이를 기반으로 경로를 선택해 특정 뉴런의 시각화 결과를 임의로 조작할 수 있는 공격 방식을 제공한다. 특히 자연 입력에 대한 모델의 성능을 유지한 채, 해석 결과만 속일 수 있다는 점에서 interpetability circumvention attack의 대표적 사례라 할 수 있다.

Manipulating visualizations through silent units

Figure 6.

두 번째로 본 논문에서는 feature visualization으로 생성된 이미지가 고주파 성분, 이상한 패턴, 비자연스러운 텍스처 등을 포함하는 경향이 있다는 점을 활용한다. 이로 인해 자연 이미지와의 분포 차이가 명확하게 존재하며, 이를 이용해 silent unit을 활용한 조작 기법을 제안한다.

Formula 1,2.

Silent unit : 전체 학습 데이터에 대해 활성화 되지 않는 유닛
- ∇𝑦 : silent unit에서의 추가 출력 (natural 이미지에서는 거의 0, feature visualization 과정에서는 활성화 됨)
- Θ : orthogonal 필터
  - 분포의 차이를 이용하여 unnatural한 이미지에 필터가 활성화 되며 활성화 시 시각화 이미지는 필터가 표현하는 이미지로 출력됨

\[\bar{y} = y + \Delta y, \quad \Delta y = \text{ReLU}(\text{Conv}(x, \bar{Θ}) + b)\]

여기서 $\bar{Θ} = αΘ + βΔΘ^{\perp}$는 기존 필터와 직교하는 새로운 필터 조합
bias $b$는 자연 이미지에서 활성화되지 않도록 충분히 큰 음수로 설정:

\[b = -\frac{α}{β} \bar{y}_{\text{max, nat}}\]

결과적으로 자연 이미지에서는 $\Delta y \approx 0$이 되어 기존 출력과 동일하고, feature visualization에서는 $\Delta y \neq 0$으로 인해 조작된 시각화 결과를 생성하게 된다.

이러한 방식은 fooling circuit처럼 복잡한 구조 없이도 기존 뉴런을 변경하지 않고, 전체 layer의 시각화를 완전히 조작할 수 있다는 장점을 가진다. 실제로 ResNet-50에서 전체 512개의 뉴런이 동일한 패턴을 시각화하도록 유도한 결과는 Figure 5에서 확인할 수 있다. 이는 시각화 기반 해석이 뉴런의 실제 계산 역할과 무관하게 보여질 수 있음을 강하게 시사한다.

Experiment

visualization

Figure 5.

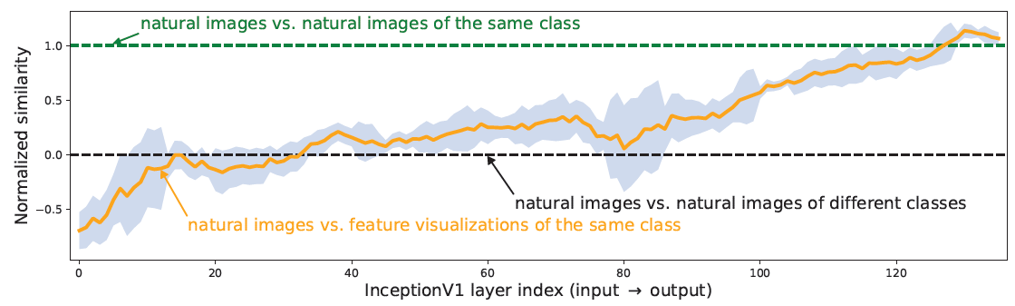
Do feature visualizations reliably reflect how standard, unmanipulated networks respond to natural input? Natural vs Synthetic path similarity analysis

Figure 4.

Natural Image와 Visualized 된 이미지의 네트워크 activation 경로 비교
- 네트워크의 앞쪽과 중간 layer는 무작위 클래스 간 비교하는 수준으로 나타남

Theory : impossible results for feature visualization

본 논문에서는 “Feature visualization만 가지고 유닛의 동작을 이해할 수 있나?“라는 질문에 대해 명확히 “불가능하다“라고 결론짓는다.
이를 뒷받침하기 위해 여러 이론적 정리를 제시하며, 왜 feature visualization이 black-box 모델을 설명하는 데 부적절한가를 보여준다.

\[Φ_{\text{min,max}}(f) = \left( \arg\min_x f(x), \arg\max_x f(x), \min_x f(x), \max_x f(x) \right)\]

Feature visualization은 위의 식과 같은 정보를 제공한다. 하지만 Feature visualization은 단순히 입력 공간 $x$에 대해 가장 작은 값과 가장 큰 값을 찾아낸 결과일 뿐, 함수 $f(x)$의 전체 구조나 동작을 파악하기에는 정보가 너무 부족하다.

Theorem 1

\[\|f' - D(Φ_{\text{min,max}}(f'))\|_{\infty} \geq \frac{f'_{\text{max}} - f'_{\text{min}}}{2}\]

함수의 복원 가능성을 확인해 보자면, 서로 다른 함수가 같은 시각화를 가질 수 있기 때문에 복원할 수 없어 시각화 결과로 유닛의 동작을 재구성 할 수 없음을 보인다.

어떤 디코더 $D$가 주어져도, 동일한 feature visualization 결과 $\Phi_{\text{min,max}}$를 갖는 두 개의 전혀 다른 함수 $f_1$, $f_2$가 항상 존재한다.
이 말은 곧, feature visualization만으로는 원래의 함수 $f(x)$를 재구성하는 것이 불가능하다는 것을 의미한다.

B.5.3. Proof of theorem 1.

$f_1$, $f_2$는 동일한 $\arg\min$, $\arg\max$, $\min$, $\max$를 가지지만,
전체 함수 모양은 완전히 다름
직관적으로, 두 함수 모두 같은 이미지를 시각화할 수 있지만, 실제로는 서로 다른 동작을 할 수 있다.

즉, 시각화는 단지 하나의 “극단값”을 보여줄 뿐이며, 함수의 전체적인 구조나 해석 가능성은 제공하지 않는다.

Theorem 2

\[\left\| \mathbb{1}_{f' > m_{f'}} - \mathbb{1}_{D(Φ_{\text{min,max}}(f')) > m_{f'}} \right\|_{\infty} \geq 1\]

“시각화 결과로 해당 입력이 positive 한지 negative한지 알 수 있나?” 라고 했을 때 동일한 시각화 결과를 보여주는 함수가 정반대의 출력을 낼 수 있기 때문에 “알 수 없다”라고 답한다.

Positive? : 입력에 대한 유닛의 출력값의 중간값 보다 높을 때를 의미
여기서 $m_{f’} = \frac{f’{\text{max}} + f’{\text{min}}}{2}$ 는 중간값 (median-like threshold)을 의미한다.
즉, feature visualization 결과를 기반으로 한 디코더 $D$는 어떤 입력 $x$에 대해 $f(x)$가 중간값 이상인지 아닌지를 정확하게 판단할 수 없다.
심지어 같은 시각화 결과를 갖는 함수 $f_1$, $f_2$가 존재하면서:
- $f_1(x) > m$,
- $f_2(x) < m$ 이 성립될 수 있다.

이는 Positive/Negative를 구분하는 가장 단순한 형태의 예측조차 시각화 정보만으로는 신뢰할 수 없다는 이론적 근거를 제공한다.

Conclusion

Feature visualization은 모델 내부를 이해하는 데 유용한 탐색적 도구일 수 있으나, 몇 가지 한계를 가진다.

Feature visualization은 시각적으로 인상적인 결과를 제공할 수는 있지만, 실제로 모델 내부의 동작이나 유닛의 의미를 “정확히” 이해할 수 있게 해주지는 않는다.
- 특히 black-box 신경망처럼 함수 형태에 제약이 없는 경우, 동일한 시각화 결과가 매우 다양한 동작을 가진 함수에서 유도될 수 있음이 수학적으로 보장된다.

따라서 feature visualization은 탐색적 분석 도구로는 쓸 수 있지만, 확정적인 설명 수단으로 사용하기에는 적합하지 않다.

Paper, Privacy

Privacy Explainable AI

This post is licensed under CC BY 4.0 by the author.